Consider a beam of length , whose weight is negligible in the elasticity equations, supported freely at

Consider a beam of length ℓ, whose weight is negligible in the elasticity equations, supported freely at both ends (so the slope of the beam is unconstrained at the ends). Show that the frequencies of standing flexural waves satisfy

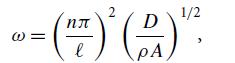
where A is the cross sectional area, and n is an integer. Now repeat the exercise when the ends are clamped. Based on your result, explain why xylophones don’t have clamped ends.

Transcribed Image Text:

(0) = пл l 2 D (2)" PA 1/2