Consider a plasma with a distribution function F(v) that has precisely two peaks, at v = v₁ and v = v₂ [with F(v₂) ≥ F(v₁)], and a minimum between them at v = v_min, and assume that the minimum is deep enough to satisfy the Penrose criterion for instability [Eq. (22.52)]. Show that there will be at least one unstable mode for every wave number k in the range k_min max, where

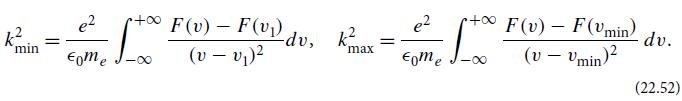
Show, further, that the marginally unstable mode at k = k_max has phase velocity ω/k = v_min, and the marginally unstable mode at k = k_min has ω/k = v₁.

k min p+ F(v) - F(v) (v - v) 1000 tome -dv, k = max e fome p+ F(v) - F(min) (v - Umin) 150 dv. (22.52)