Consider fully thermalized electromagnetic radiation at temperature T , for which the mean occupation number has the standard Planck (blackbody) form = 1/(e x

Consider fully thermalized electromagnetic radiation at temperature T , for which the mean occupation number has the standard Planck (blackbody) form η = 1/(e^x − 1) with x = hν/(k_BT).(a) Show that the entropy per mode of this radiation is

(b) Show that the radiation’s entropy per unit volume can be written as the following integral over the magnitude of the photon momentum:

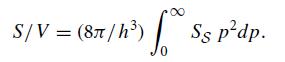
(c) By performing the integral (e.g., using Mathematica), show that

where U = aT 4 is the radiation energy density, and a = (8π⁵k⁴_B/15)/(ch)3 is the radiation constant

(d) Verify Eq. (4.39) for the entropy density by using the first law of thermodynamics dE = T dS − PdV

Ss=kB[x/(et - 1) - In(1-e*)].