Consider monochromatic electromagnetic waves that propagate from a medium with index of refraction n₁ into a medium with index of refraction n₂. Let z be a Cartesian coordinate perpendicular to the planar interface between the media.

(a) From the Helmholtz equation [−ω² + (c²/n²)∇²]ψ = 0, show that both ψ and ψ,_z must be continuous across the interface.

(b) Using these continuity requirements, show that for light propagating orthogonal to the interface (z direction), the reflection and transmission coefficients, in going from medium 1 to medium 2, are

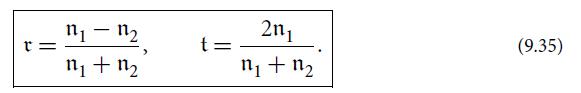
Notice that these r and t are both real.

(c) Use the reciprocity relations (9.34) to deduce the reflection and transmission coefficients r' and t' for a wave propagating in the opposite direction, from medium 2 to medium 1.

= 1-1 1 + 1 2n n + 1 (9.35)