Consider the secondary wave generated by

the holographic reconstruction process of Fig. 10.8, Eq. (10.7), and Ex. 10.2.

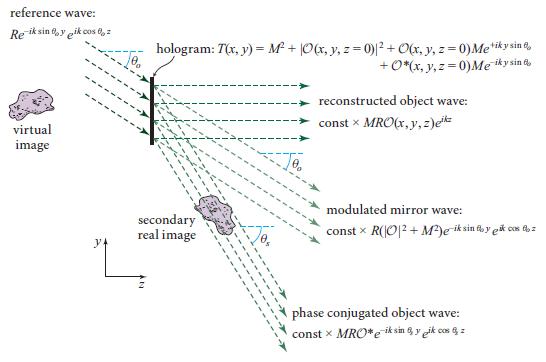
(a) Assume, for simplicity, that the mirror and reference waves propagate nearly perpendicular to the hologram, so θo « 90◦ and θ_s ≈ 2θo « 90◦; but assume that θ_s is still large enough that fairly far from the hologram the object wave and secondary waves separate cleanly from each other. Then, taking account of the fact that the object wave field has the form O(x, y, z)e^ikz, show that the secondary wave is the phase-conjugated object wave defined in this section, except that it is propagating in the +z direction rather than −z (i.e., it has been reflected through the z = 0 plane). Then use this and the discussion of phase conjugation in the text to show that the secondary wave carries an image that resides in front of the hologram and is turned inside out, as discussed near the end of Sec. 10.3. Show, further, that if θo is not90◦ (but is s is a real angle, and the secondary image actually exists), then the secondary image is changed by a distortion along the y direction. What is the nature of the distortion, a squashing or a stretch?

(b) Suppose that a hologram has been made with θ_o

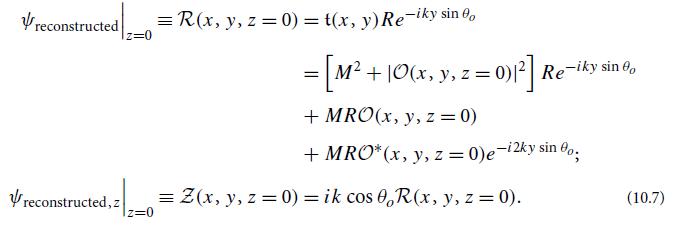
Data from Exercises 10.2

Fig. 10.8

tx MO*e-iky sin 80