Derive Eq. (11.55) relating the angle o = (d/dx) x = 0 = k o = o / to the applied force F

Derive Eq. (11.55) relating the angle θ_o = (dη/dx)_{x = 0} = kη_o = πη_o/ℓ to the applied force F when the card has an n = 1, arched shape.

(a) Derive the first integral of the elastica equation

where θ_o is an integration constant. Show that the boundary condition of no bending torque (no inflection of the card’s shape) at the card ends implies θ = θ_o at x = 0 and x = ℓ; whence θ = 0 at the card’s center, x = ℓ/2.

(b) Integrate the differential equation (11.59) to obtain

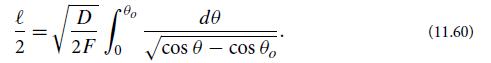
(c) Perform the change of variable sin(θ/2) = sin(θ_o/2) sin ∅ and thereby bring Eq. (11.60) into the form

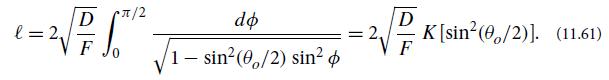
Here K(y) is the complete elliptic integral of the first type, with the parameterization used by Mathematica (which differs from that of many books).

(d) Expand Eq. (11.61) in powers of θ_o/2 to obtain

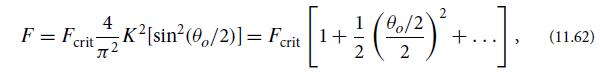
from which deduce our desired result, Eq. (11.55).

Eq. (11.55)

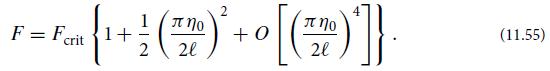
(de/dx) = 2(F/D) (cos 0 - cos 0), (11.59)