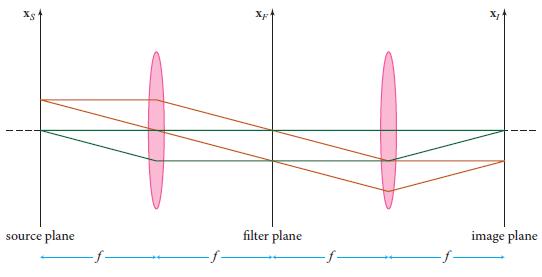
Question: Figure 8.17 depicts a two-lens system for spatial filtering (also sometimes called a 4f system, since it involves five special planes separated by four intervals
Figure 8.17 depicts a two-lens system for spatial filtering (also sometimes called a “4f system,” since it involves five special planes separated by four intervals with lengths equal to the common focal length f of the two lenses). Develop a description, patterned after Abbes, of image formation with this system. Most importantly, do the following.(a) Show that the field at the filter plane is
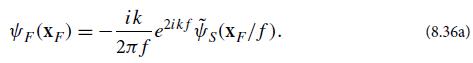
This is like Eq. (8.31) for the one-lens system but with the spatially dependent phase factor exp[−ikxF2 /(2(v − f))] gone, so aside from a multiplicative constant, the filter-plane field is precisely the Fourier transform of the source-plane field.
(b) In the filter plane we place a filter whose transmissivity we denote K̃(−xF/f), so it is (proportional to) the filter-plane field that would be obtained from some source-plane field K(−xS). Using the optics conventions (8.11) for the Fourier transform and its inverse, show that the image-plane field, with the filter present, is
![]()
Here ψS is the convolution of the source field and the filter function
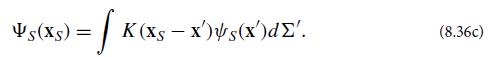
In the absence of the filter, ψS is equal to ψS, so Eq. (8.36b) is like the image plane field (8.33) for the single-lens system, but with the spatially dependent phase factor exp[−ikx2F/(2(v − f))]gone. Thus ψ1 is precisely the same as the inverted ψS, aside from an overall phase.
Fig. 8.17
Equations
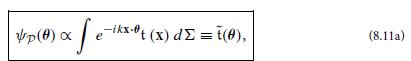
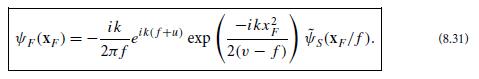
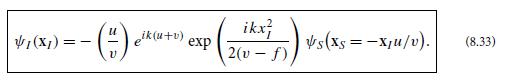
VF(XF) = ik -eikf s(XF/f). 2 f (8.36a)
Step by Step Solution
3.39 Rating (158 Votes )
There are 3 Steps involved in it
Solution a Field at the Filter Plane First we need to understand how the field propagates from the source plane to the filter plane in the 4f system C... View full answer

Get step-by-step solutions from verified subject matter experts


