For = 3 and for a channel with A = A (1+ x 2 ), solve the flow equations (1) of Box 17.3

For γ = 3 and for a channel with A = A_∗(1+ x²), solve the flow equations (1) of Box 17.3 analytically and explicitly for v(x), and verify that the solutions have the qualitative forms depicted in the last figure of Box 17.3.

Box 17.3.

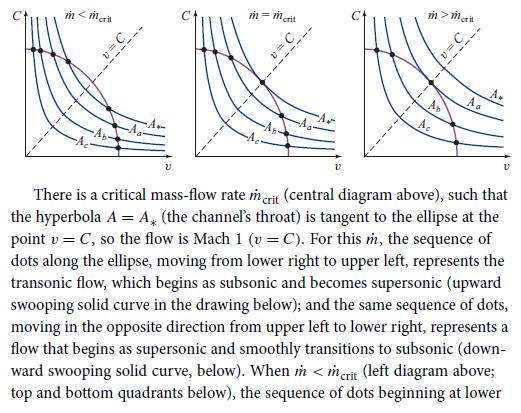
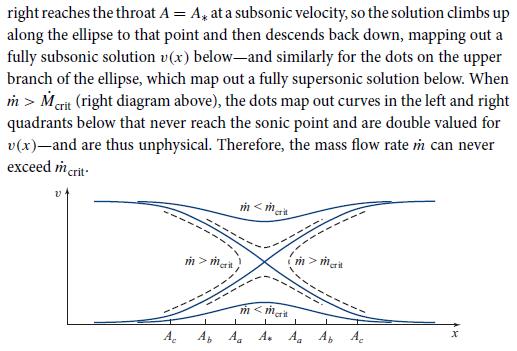
BOX 17.3. VELOCITY PROFILES FOR 1-DIMENSIONAL FLOW BETWEEN CHAMBERS Consider the adiabatic, stationary flow of an isentropic, polytropic fluid P = Kp" between the two chambers shown in Fig. 17.5. Describe the channel between chambers by its cross sectional area A (x) as a function of distance x, and describe the flow by the fluid's velocity v(x) and its sound speed C(x). There are two coupled algebraic equations for v(x) and C (x): mass conservation pu A = m [Eq. (17.4a)] and the Bernoulli theorem h + {/v = h [Eq. (17.4c)], which, for our polytropic fluid, become [see Eqs. (17.2d)]: c/(x-)= (y K)/(x-m/A, These equations are graphed in diagrams below for three different mass flow rates m. Mass conservation [the first of Eqs. (1)] is a set of generalized hyperbolas, one for each value of the channel's area A, < Aa < Ap < Ac. The Bernoulli theorem [the second of Eqs. (1)] is a single ellipse. On a chosen diagram (for a chosen m), the dot at the intersection of the ellipse with a hyperbola tells us the flow velocity v and speed of sound C at each of the two points in the channel where the area A has the hyperbola's value. C 22 c Y-1 + = y - 1 2 (1)