Here is an example of how to use index notation to derive a vector identity for the double cross product A × (B × C): in index notation this quantity is ∈_{ij k}A_j (∈_klmB_lC_m). By permuting the indices on the second ∈ and then invoking Eq. (1.23), we can write this as

By then invoking the meaning of the 4-index delta function [Eq. (1.23)], we bring this into the form A_jB_iC_j − A_jB_jC_i, which is the slot-naming index-notation form of (A · C)B − (A · B)C. Thus, it must be that A × (B × C) = (A · C)B− (A · B)C. Use similar techniques to evaluate the following quantities.(a) ∇ × (∇ × A).(b) (A × B) · (C × D).(c) (A × B) × (C × D).

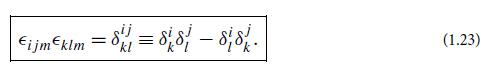
EijkelmkAjBCm=8m A; BCm-