In Sec. 7.5, we explored five elementary (generic) caustics that can occur in geometric optics. Each is described by its phase φ(ã , b̃; x̃, ỹ, z̃) for light arriving at an observation point with Cartesian coordinates {x̃, ỹ, z̃} along paths labeled by (ã , b̃).

(a) Suppose the (monochromatic) wave field ψ(x̃ , ỹ , z̃) that exhibits one of these caustics is produced by plane-wave light that impinges orthogonally on a phase shifting surface on which are laid out Cartesian coordinates (ã , b̃). Using the Helmholtz-Kirchhoff diffraction integral (8.6), show that the field near a caustic is given by

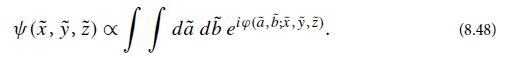
(b) In the text we evaluated this near-caustic diffraction integral for a fold caustic, obtaining the Airy function. For the higher-order elementary caustics, the integral cannot be evaluated analytically in terms of standard functions. To get insight into the influence of finite wavelength, evaluate the integral numerically for the case of a cusp caustic,

and plot the real and imaginary parts of

Before doing so, though, guess what these parts will look like. As foundations for this guess, 

(i) Pay attention to the shape x̃ =±2(z̃/3)^3/2 of the caustic in the geometric-optics approximation, 

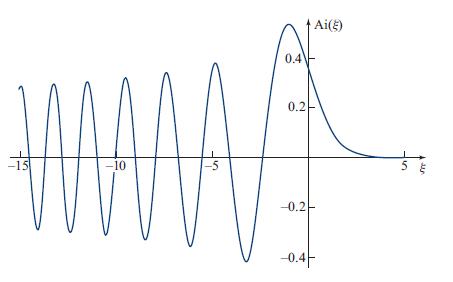
(ii) Notice that away from the cusp point, each branch of the caustic is a fold, whose ψ is the Airy function (Fig. 8.19), 

(iii) Note that the oscillating ψ associated with each branch interferes with that associated with the other branch. The numerical computation may take awhile, so make a wise decision from the outset as to the range of z̃ and x̃ to include in your computations and plots. If your computer is really slow, you may want to prove that the integral is symmetric in x̃ and so restrict yourself to positive x̃ , and argue that the qualitative behaviors ofRψ and Jψ must be the same, and so restrict yourself to Rψ.

Fig. 8.19

Transcribed Image Text:

af fa dã dỗ eip(a,brĩ,ỹ,2) v (x, y, z) x (8.48)