Show that for thermalized, classical relativistic particles the probability distribution for the speed is

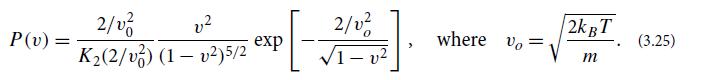
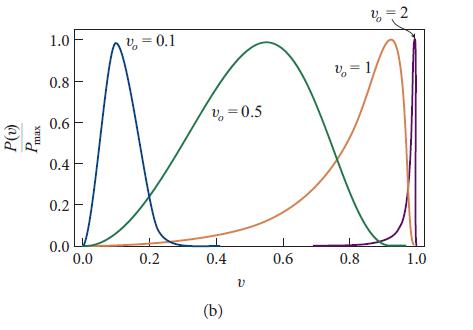
Where K₂ is the modified Bessel function of the second kind and order 2. This is sometimes called the Maxwell-Jutner distribution, and it is plotted in Fig. 3.6b for a sequence of four temperatures ranging from the nonrelativistic regime k_BT ≪  m toward the ultrarelativistic regime kBT >> m. In the ultrarelativistic regime the particles are (almost) all moving at very close to the speed of light, v = 1.

Fig 3.6 (b)

P(v) = = 2/0 v K(2/v) (1-v)5/2 exp 2/0 - v 3 where vo= 2k BT m (3.25)