Show that the Euler-Lagrange equation for the action principle (27.8) is equivalent to the geodesic equation for a photon in the static spacetime metric g₀₀(x^k), g_ij(x^k). Specifically, do the following.

(a) The action (27.8) is the same as that for a geodesic in a 3-dimensional space with metric γ_jk and with t playing the role of proper distance traveled [Eq. (25.19) converted to a positive-definite, 3-dimensional metric]. Therefore, the Euler- Lagrange equation for Eq. (27.8) is the geodesic equation in that (fictitious) space [Eq. (25.14) with t the affine parameter]. Using Eq. (24.38c) for the connection coefficients, show that the geodesic equation can be written in the form

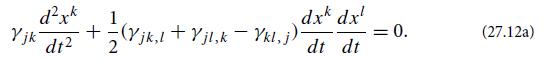
(b) Take the geodesic equation (25.14) for the light ray in the real spacetime, with spacetime affine parameter ζ, and change parameters to coordinate time t. Thereby obtain

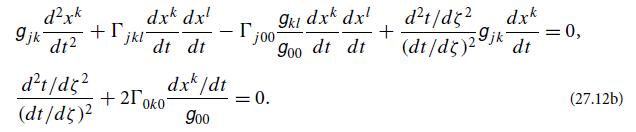
(c) Insert the second of these equations into the first, and write the connection coefficients in terms of derivatives of the spacetime metric. With a little algebra, bring your result into the form Eq. (27.12a) of the Fermat-principle Euler-Lagrange equation.

Equations.

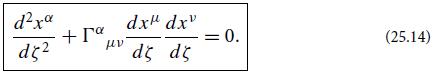
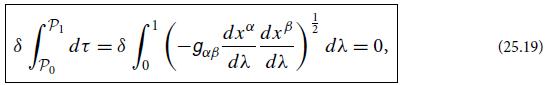
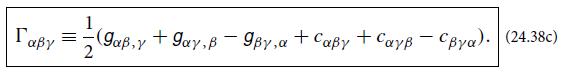
dxk Yjk dt 1 - -/- (Yjk,l + Y jl,k - Ykl, j) = 0. dxk dx dt 2 dt (27.12a)