Suppose that a stress T_zj^applied (x_o) is applied on the face z = 0 of a half-infinite elastic body (one that fills the region z >0). Then by virtue of the linearity of the elastostatics equation f = (K + 1/3μ)∇(∇ · ξ) + μ∇²ξ = 0 and the linearity of its boundary conditions, T_zj^internal = T_zj^applied, there must be a Green’s function G_jk(x − x_o) such that the body’s internal displacement ξ(x) is given by

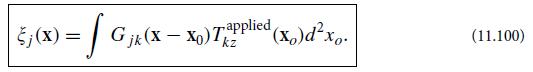
Here the integral is over all points xo on the face of the body (z = 0), and x can be anywhere inside the body, z ≥ 0.(a) Show that if a force F_j is applied on the body’s surface at a single point (the origin of coordinates), then the displacement inside the body is

Thus, the Green’s function can be thought of as the body’s response to a point force on its surface.

(b) As a special case, consider a point force F_z directed perpendicularly into the body. The resulting displacement turns out to have cylindrical components¹²

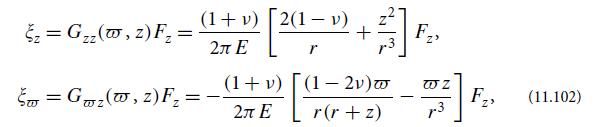
where

It is straight forward to show that this displacement does satisfy the elastostatics equations (11.92). Show that it also satisfies the required boundary condition

 

(c) Show that for this displacement [Eq. (11.102)], 

vanishes everywhere on the body’s surface z = 0 except at the origin ω̅ = 0 and is infinite there. Show that the integral of this normal stress over the surface is F_z, and therefore, T_zz(z = 0) = F_zδ₂(x), where δ₂ is the 2-dimensional Dirac delta function on the surface. This is the second required boundary condition.

(d) Plot the integral curves of the displacement vector ξ (i.e., the curves to which ξ is parallel) for a reasonable choice of Poisson’s ratio ν. Explain physically why the curves have the form you find.

(e) One can use the Green’s function (11.102) to compute the displacement ξ induced by the Gaussian-shaped pressure (11.89) applied to the body’s face, and to then evaluate the induced expansion and thence the thermoelastic noise; see Braginsky, Gorodetsky, and Vyatchanin (1999) and Liu and Thorne (2000). The results agree with Eqs. (11.97) and (11.98) deduced using separation of variables.

Equations

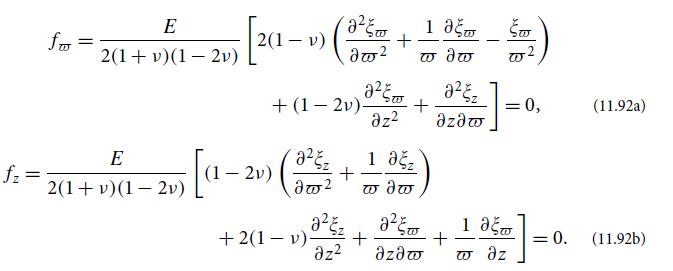
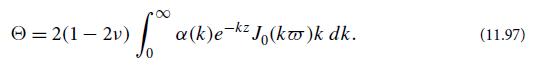
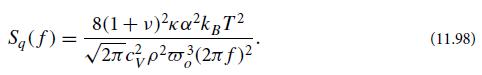
j (X) = [G = (x)dxo. Gjk (X-Xo) 7applied (11.100)