Consider the single-input, single-output system described bywhere r(t) is the reference input. The matrix K = [K1 K2 ] is known as the gain matrix. Substituting u(t) into the state variable equation gives the closed-loop system x (t) = [A −BK]x(t)+ Br(t)

y(t) = Cx(t).

The design process involves finding K so that the eigenvalues of A-BK are at desired locations in the left-half plane. Compute the characteristic polynomial associated with the closed-loop system and determine values of K so that the closed-loop eigenvalues are in the left-half plane.

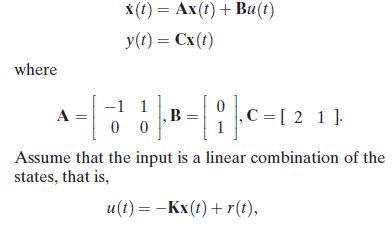
x(t) = Ax(t) + Bu(t) y(t) = Cx(t) where -1 1 A B ,C=[ 21 ]. =1211 00 Assume that the input is a linear combination of the states, that is, u(t) = -Kx(t)+r(t),