A cosmic string is a one-dimensional object with an extraordinarily large linear mass density ( 10 22 kg/m) which (in some theories) formed during

A cosmic string is a one-dimensional object with an extraordinarily large linear mass density (μ ∼ 10²² kg/m) which (in some theories) formed during the initial cool-down of the Universe after the Big Bang. In two-dimensional (2D) general relativity, such an object distorts flat spacetime into an extremely shallow cone with the cosmic string at its apex. Alternatively, one can regard flat 2D space as shown below: undistorted but with a tiny wedge-shaped region removed from the physical domain. The usual angular range 0 ≤ φ −1 = 1 − 4Gμ/c², G is Newton’s gravitational constant, and c is the speed of light. The two edges of the wedge are indistinguishable so any physical quantity f (φ) satisfies f (0) = f (2π/p) .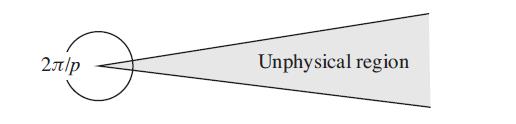

(a) Begin with no string. Show that the free-space Green function in 2D is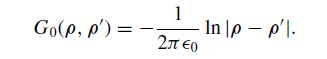

(b) Now add the string so p ≠1. To find the modified free-space Green function G^p₀ (ρ, ρ'), a representation of the delta function is required which exhibits the proper angular behavior. Show that a suitable form is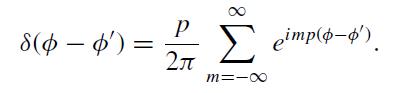

(c) Exploit the ansatz.

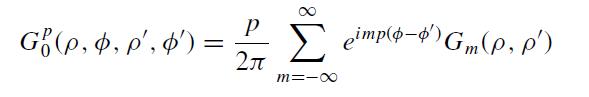
To show that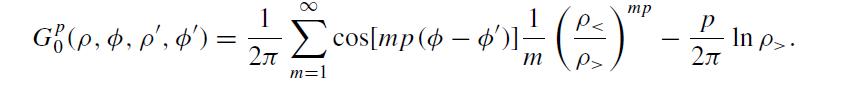

(d) Perform the indicated sum and find a closed-form expression for G^p₀. Check that G¹₀ (ρ, ρ') correctly reproduces your answer in part (a).

(e) Show that a cosmic string at the origin and a line charge q at ρ are attracted with a force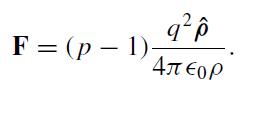

2T/P Unphysical region