A current I flows up the z-axis and is intercepted by an origincentered sphere with radius R and conductivity . The current enters and exits

A current I flows up the z-axis and is intercepted by an origincentered sphere with radius R and conductivity σ. The current enters and exits the sphere through small conducting electrodes which occupy the portion of the sphere’s surface defined by θ ≤ α and π − α ≤ θ ≤ π. Derive an expression for the resistance of the sphere to the flowing current. Assume that α >> 1 and comment on the limit α → 0.

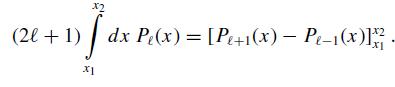
x2 (2+1) dx P(x) = [P+1(x) - P-1(x) XI -