(a) Derive an integral expression for the charge density (, z) induced on the outer surface of a conducting tube of radius R when a

(a) Derive an integral expression for the charge density σ(φ, z) induced on the outer surface of a conducting tube of radius R when a point charge q is placed at a perpendicular distance s > R from the symmetry axis of the tube.

(b) Confirm that the point charge induces a total charge −q on the tube surface.

(c) Show that the angle-averaged linear charge density falls off extremely slowly with distance along the length of the tube. Specifically, show that, as z→∞,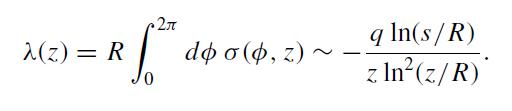

2 R 1.Th S (z) = R d (,z) ~ q ln(s/R) z ln(z/R)