A plane electromagnetic wave EI cos(k I z + I t) is incident on a perfectly reflecting mirror (solid line) that moves with constant

A plane electromagnetic wave EI cos(k_Iz + ω_It) is incident on a perfectly reflecting mirror (solid line) that moves with constant velocity v = νẑ. The reflected plane wave is ER cos(k_Rz − ω_Rt).

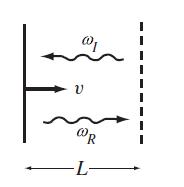
(a) Use conservation of momentum to show that the force exerted on an area A of the mirror is

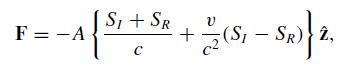
where S is the magnitude of the Poynting vector. When ν = 0, the electromagnetic momentum in the volume between the mirror and any fixed reference plane (dashed line) changes in time.

(b) Use conservation of energy to show that

F · ν = A(S_I − S_R) + A(S_I+ S_R)v/c.
(c) From (a) and (b), deduce that the reflected energy/time PR that flows through a fixed reference plane (dashed line) exceeds the incident energy/time PI that flows through the same plane by the ratio

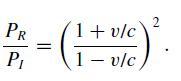
(d) Relate the phase of the incident and reflected waves at the surface of the mirror (z = νt). Use this relation to deduce that P_R/P_I = (ω_R/ω_I)².

@01 V COR -L-