(a) Separate variables in cylindrical coordinates and find a general time-harmonic solution (,, z, t) of the scalar wave equation which propagates in the z-direction

(a) Separate variables in cylindrical coordinates and find a general time-harmonic solution ψ(ρ,φ, z, t) of the scalar wave equation which propagates in the z-direction and remains finite on the z axis. 

(b) Find the TE and TM electric and magnetic fields associated with the magnetic Hertz vector πm = ψ₀ ẑ where ψ₀ is the cylindrically symmetric solution found in part (a).
(c) Interpret ψ₀(r, t) as a sumof planewaves exp[i(q · r − ωt)] where the q vectors have the same magnitude and are distributed uniformly on the surfaced of a cone.

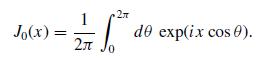
Jo(x) = 2 11/12 1 0 de exp(ix cos 0). 2