An electromagnetic wave E = E exp(it) can induce a net magnetization in a metal. To see this, let the density and velocity of the

An electromagnetic wave E = δE exp(−iωt) can induce a net magnetization in a metal. To see this, let the density and velocity of the electrons at a typical point be n =  + δn exp(−iωt) and v = v̅ + δv exp(−iωt ), where n̅ is the mean density of the electrons and v̅ = 0 is the mean velocity of the electrons. The current density j = −e n̅ v has two time-dependent pieces, one of which is δ j = −e n̅ δ v = σ δ E, where σ = i n̅ e² / mω is the collisionless Drude conductivity.

(a) Show that the time-averaged current density is (j) = −1 / 2Re {eδnδv∗}.
(b) Evaluate δn to first order in δv (using the continuity equation) and show that a piece of (j) has the form ∇ × M where (the plasma frequency is defined by ω²_p = ne²/mϵ₀)

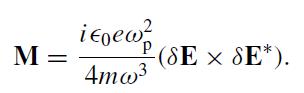
(c) Evaluate M when δE is linearly polarized. Repeat for circular polarization.

M = ieoew 4mw3 -(SE SE*).