An infinite slab with dielectric constant 0 lies between z a and z b a c A point charge q sits at the origin of coordinates Let ( 1) ( 1) and use solutions of Laplaces equation in cylindrical coordinates to show that 4(z c) q(1 B) S 0 dk Jo(kp) exp( kz) 1 B exp( 2kc) q(1 B) n 0 Bn (z 2nc) p

Question: An infinite slab with dielectric constant = / 0 lies between z = a and z = b = a + c. A point

An infinite slab with dielectric constant κ = ε/ε₀ lies between z = a and z = b = a + c. A point charge q sits at the origin of coordinates. Let β = (κ − 1)/(κ + 1) and use solutions of Laplace’s equation in cylindrical coordinates to show that.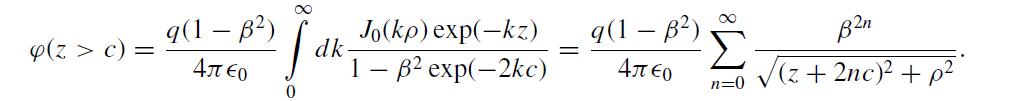 4(z > c) = q(1 - B) S 0 dk Jo(kp) exp(-kz)

4(z > c) = q(1 - B) S 0 dk Jo(kp) exp(-kz) 1 -B exp(-2kc) = q(1 - B) n=0 Bn (z+2nc) + p

Step by Step Solution

★★★★★

3.31 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

From Section 832 we recall that Then in Regio... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Electrodynamics Questions!

A rhinoceros is at the origin of coordinates at time I, = O. For the time interval from I, = 0 to 12 = 12.0 s, the rhino's average velocity has x-component -3.8 m/s and y-component 4.9 m/s. At time...

A 3-cm-wavelength radar is located at the origin of an xy coordinate system. A car located at x = 100 m and y = 200 m is heading east (x-direction) at a speed of 120 km/hr. What is the Doppler...

A vessel at rest at the origin of an xy coordinate system explodes into three pieces. Just after the explosion, one piece, of mass m, moves with velocity (-30 m/s)i and a second piece, also of mass...

Saved CHECK ANSWER 2 of Unlimited checks used Question 11 (1 points) (#212193) {Continuous Distributions of Charge} An infinite horizontal plane of uniform negative charge sits at a height of z = 0....

|Assignment 2 Student Name: ... ... . ] 1. At coordinates (0,1), a charge of -1.0 yC exists on the y-axis, 1.0 m from the origin, and at coordinates (1,0), on the x-axis, 1.0 m from the origin, is a...

a) A linear charge density = 4z C/m is distributed on the z axis, what is the total charge within a cylinder of radius r = 0.5 m and height h = 5 m which extends from z = 1 to z = 4? b) A uniform...

space weather PLEASE HELP ME use MATLAB NO REFERENCE 1.1 Free Space Maxwell's equations describe the behavior of electromagnetic fields and their interaction with mat- ter. They are one of the major...

A thin plastic rod of length d = 1.5 m lies along the x -axis with its midpoint at the origin. The rod carries a uniform charge density of ? = 3.5 nC/m. The point P is located along the y -axis at...

(Multiple choice) (1) A lithium nucleus and an ? particle are at rest. The lithium nucleus has a charge of +3e and a mass of 7 u; the ? particle has a charge of +2e and a mass of 4 u. Which of the...

Problem 1: An infinite slab of charge of thickness 22, lies in the xy-plane between z = -2, and z = +20. The volume charge density p (C/m ) is a positive constant. Find the electric field everywhere...

In reference to a company sharing information that it has collected about a customer, what is meant by opt in? By opt out? In your opinion, which of these is preferable?

Choose a company you are familiar with and examine how efficiently or effectively it has designed the procurement, production, and transportation aspects of its businesses.

An example of the command-and-control approach to environmental policy is a. placing a tax on Freon to reduce its use and the corresponding CFC emissions (which contribute to the ozone hole). b....

Microsofts mission is to enable people and businesses throughout the world to realize their full potential by creating technology that transforms the way people work, play and communicate. The...

Beginning from their definitions, determine the conversion factor between ft lb and kW h in Table 7.1. Table 7.1 ft- Ib Btu kW -h 1 1.356 1.285 x 10-3 3.766 x 10-7 0.7376 1 9.478 x 10-4 2.778 x...

A remote-controlled toy car weighs 3 lb and moves at 15 ft/s. What is its kinetic energy?

A lawn mower engine is started by pulling a cord wrapped around a hub of radius 6.0 cm. If a constant tension of 80 N is maintained in the cord and the hub makes three revolutions before the motor...

Why do some prospective wholesale borrowers and lenders hedge using derivative contracts? O Because hedging will always result in a better outcome Because derivatives can be used to offset a risk in...

Accounts receivable changes without bad debts Tara's Textiles currently has credit sales of $ 3 6 0 million per year and an average collection period of 5 9 days. Assume that the price of Tara's...

Victoria Bassett is from Syracuse, New York and she has a $88, 250 gross income. What amount of taxes on a gross income will she pay? She paid $ in taxes on a gross income. An average tax rate would...