At a single space-time point, it is always possible to orient the space axes so E_z = B_z
= 0 and E · B = EB cos θ.

(a) Under these conditions, diagonalize μν and show that the two distinct eigenvalues are

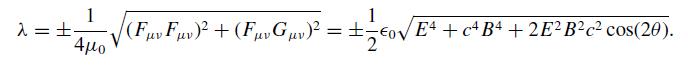
(b) Show that part (a) implies that the electromagnetic energy density at the space-time point in question is either zero or not less than |λ| in every inertial frame.

1 = - = 42 (Fv Fv) + (FvGv) = = 0/E +c4B + 2E Bc cos(20).