Consider time-harmonic electromagnetic fields in the domain z ≥ 0 of the form

(a) Let ŷ · E_TE(x, z = 0, t = 0) = E̅_y (x). Determine the scalar function Λ_TE(k_x) and the vector function TE(k_x) so that

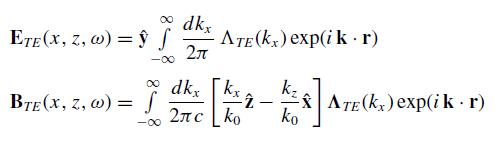
solve Maxwell’s equations in free space. The wave vector k = x̂ k_x + ẑ k_z is two-dimensional. Explain why there is no integral over k_z.

(b) Let x̂ · ETM(x, z = 0, t = 0) = E̅x (x). Determine the scalar function Λ_TM(k_x) and t

he vector function "Γ_TM(k_x) so that

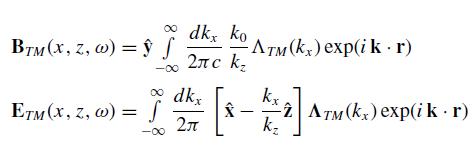
solve Maxwell’s equations in free space. The factor k₀ = ω/c.

(c) Represent a general z ≥ 0 field as E = E_TE + E_TM and B = B_TE + B_TM. If S is the Poynting vector, show that the time-averaged power transmitted down the z-axis is

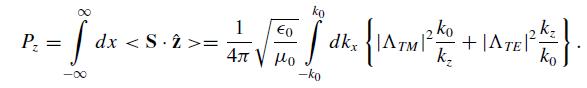
What is the physical origin of the limits of integration on the kx integral?

E(x, z 0, t) = E(x, z, w) exp(-iwt) B(x, z 0, t) = B(x, z, w) exp(-iwt).