Let d be the separation between two infinite, parallel, perfectly conducting plates. The lower surface of the upper plate has charge per unit area σ₁ > 0. The upper surface of the lower plate has charge per unit area σ₂ > 0. At a distance L above the lower plate, there is an infinite sheet of charge with charge per unit area σ₀ = − (σ₁ + σ₂). If we approximate the latter by a two-dimensional electron gas, elementary statistical mechanics tells us that the energy per unit area of the sheet is u₀ = πћ²σ²₀ /2me².

Fix σ₁ and show that the total energy per unit area of the system is minimized when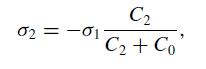

Where C₂ is a characteristic geometric capacitance and C₀ is the “quantum capacitance” of the two dimensional electron gas. Discuss the classical limit of C₀ and confirm that the corresponding value for σ₂ makes sense.

02-01 = C C + Co'