Let E inc = e 0 E 0 exp[i(kz t)] be the electric field of a planewave propagating in a homogeneous dielectric medium. The

Let E_inc = e₀E₀ exp[i(kz − ωt)] be the electric field of a planewave propagating in a homogeneous dielectric medium. The wave vector k = nk₀ = nω/c, where n is the index of refraction
of the medium. Suppose that the number density of scatters increases from N to N + δN in a thin layer of the medium between z = 0 and z = δt. Because δt is infinitesimal, E_inc scatters once from every extra atom in the layer. Therefore, if the atomic scattering amplitude is f(θ,φ), the extra electric field produced at the distant observation point z >> δt is

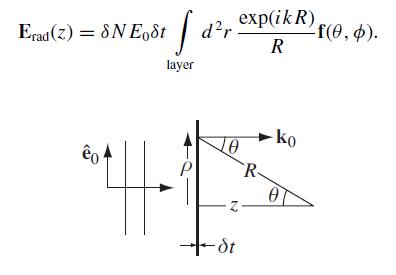
(a) Change variables to η = R/z, integrate by parts, and compare the original integral to the new integral in the limit kz >> 1. Note that f(0) ≡ f(θ = 0, φ) does not depend on φ and establish that

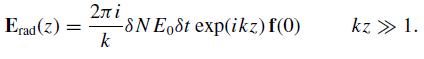
(b) Construct E(z) = E_inc(z) + E_rad(z) from the results of part (a) and argue that your expression remains valid at z = δt. Derive from this fact an expression for δk/δN, the change in wave vector induced by the density perturbation. Integrate and conclude that the index of refraction of the unperturbed medium satisfies

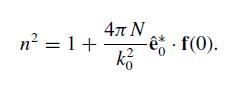
Erad (2) 8N Eo8t = o [dr layer exp(ik R) R 10 Z - St R -ko 0 -f(0, p).