Let n be the normal to an equipotential surface at a point P. The principal radii of

Let ˆn be the normal to an equipotential surface at a point P. The principal radii of curvature of the surface at P are R₁ and R₂. A formula due to George Green relates normal derivatives (∂/∂n ≡ ˆn · ∇) of the potential φ(r) (which satisfies Laplace’s equation) at the equipotential surface to the mean curvature of that equipotential surface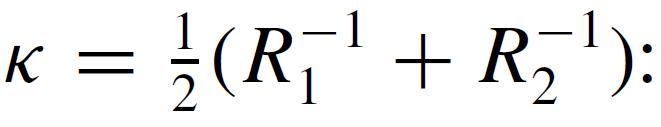

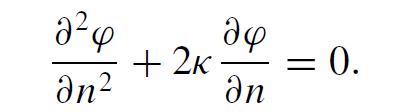
Derive Green’s equation by direct manipulation of Laplace’s equation.

Transcribed Image Text:

K = 1 ½ (R₁¹ + R₂¹):