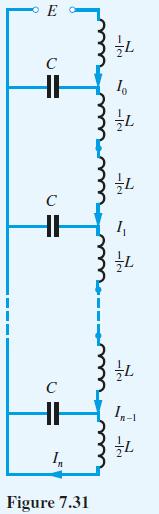
Question: A complex voltage E is applied to the ladder network of Figure 7.31. Show that the (complex) mesh currents I k satisfy the equations Show
A complex voltage E is applied to the ladder network of Figure 7.31. Show that the (complex) mesh currents Ik satisfy the equations
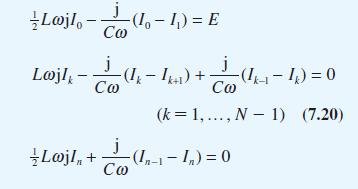
Show that
![]()
satisfies (7.20) provided that cosh θ = 1 – 1/2 LCω2. Note that this equation yields two values for u, so that in general Ik may be written as
![]()
where A and B are independent of k. Using the special equations for I0 and In, obtain the values of A and B and prove that
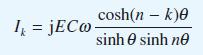
Lojl- - (1 - 1) = E Lojl, + Co j Lojl- - (1k - Ik+1) + Co j Co j Co -(1-1-1) = 0 (k = 1,..., N 1) (7.20) -(In-1-In) = 0 -
Step by Step Solution
3.43 Rating (153 Votes )
There are 3 Steps involved in it
Equation 2 I12LCIIk1 0 LCalo Io11 EC LCafIk IIk1 I1I 0 k1 ... View full answer

Get step-by-step solutions from verified subject matter experts


