A curve C in three dimensions is given parametrically by (x(t), y(t), z(t)), where t is a

Question:

A curve C in three dimensions is given parametrically by (x(t), y(t), z(t)), where t is a real parameter, with a ≤ t ≤ b. Show that the equation of the tangent line at a point P on this curve where t = t₀ is given by

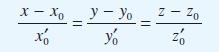
XXoy Yo - = xo Yo z - Zo zo

where x₀ = x(t₀), x´0 = x´(t₀), and so on. Hence find the equation of the tangent line to the circular helix

at t = 1/4π and show that the length of the helix between t = 0 and t = 1/2π is πa/√2.

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Related Book For answer-question

Modern Engineering Mathematics

ISBN: 9781292253497

6th Edition

Authors: Glyn James

See More Books

Question Posted: Jan 16, 2024 03:01 AM

See More Questions

To help determine the need for more golf courses, a survey was undertaken. A sample of 75 self-declared golfers was asked how many rounds of golf they played last year. These data are as follows: a....
Let the function be defined on the interval [0, 2] as follows: Determine the constants a, b, c, and d so that function ? satisfies the following : (i) ? (0) = ? (2) = 1. (ii) ??is continuous on the...
Plateau Pharmaceuticals Limited (Plateau), is a Namibian publicly listed company in the Health sector. Plateau, manufactures medical drugs for sale to various pharmacies (retail outlets) and to...
The comparative balance sheet of Merrick Equipment Co. for December 31, 20Y9 and 20Y8, is as follows: Dec. 31, 20Y9 Dec. 31, 20Y8 Assets Cash $70,720 $47,940 Accounts receivable (net) 207,230 188,190...
Hydrogen is produced in the steam reforming of propane: C 3 H 8 (g) + 3 H 2 O (v) ? 3 CO 2 (g) + 7 H 2 (g) the water?gas shift reaction also takes place in the reactor, leading to the formation of...
1. Three cars, a Mazda, a Honda, and a Ford, are in a quarter-mile race. The probability that the Mazda will win the race is 2/3, and the probability that the Honda will win is 1/4. Assuming no ties...
This appeal involves the validity of a will executed in contravention of an earlier contract to make mutual wills. A husband and wife signed a contract to make mutual wills and then executed those...
Copa Corporations accountant left for vacation before completing the monthly cost variance report. The corporations president has asked you to complete the report. The following data are available...
The threshold frequency v0 describes the smallest light frequency capable of ejecting electrons from a metal. Determine the minimum energy E0 of a photon capable of ejecting electrons from a metal...
Show that u = f(x + y) + g(x y) satisfies the differential equation n-e n-e 2 xe = 0
(a) Find the value of the positive constant c for which the function satisfies the equation (b) V is a function of the independent variables x and y. Given that x = r cos and y = r sin , find V/u...
This ethical dilemma concerns a hypothetical situation regarding various ethical issues commonly encountered within the workplace. Have students read the scenario provided in the text and then...
A firm has a fixed cost of $100,000, and variable cost is $90,000 at an output of one. How much is marginal cost at an output of one? a) $10,000 b) $90,000 c) $100,000 d) $190,000 e) There is...
Parkinsons l aw is an example of _______. a) economies of scale b) diseconomies of scale c) Adam Smiths pin factory d) the firms search for its most profitable output.
A perfectly elastic supply curve is ______. a) a horizontal line b) a vertical line c) neither a horizontal nor a vertical line
When Kelly Ziegenfuss buys five units of a particular good or service, _______. a) she has no consumer surplus b) she has a consumer surplus c) there is no way of knowing whether she has a consumer...
When demand is relatively inelastic and supply is relatively elastic, the burden of a tax will be borne ______. a) mainly by sellers b) mainly by buyers c) equally between sellers and buyers d) it is...
Surf-The-Net.com had the following events occur during October: 1. Paid $5,800 for utilities. 2. Made cash sales to customers that totaled $89,460. The merchandise had cost Surf-The-Net.com $60,000...
MgO prevents premature evaporation of Al in a furnace by maintaining the aluminum as Al2O3. Another type of matrix modifier prevents loss of signal from the atom X that readily forms the molecular...
The hollow shaft has the cross section shown and is made of an elastic perfectly plastic material having a yield shear stress of t Y . Determine the ratio of the plastic torque T p to the maximum...
A circular shaft having a diameter of 4 in. is subjected to a torque of 250 kip # in. If the material is elastic perfectly plastic, with Y = 16 ksi, determine the radius of the elastic core.
The shaft is subjected to a maximum shear strain of 0.0048 rad. Determine the torque applied to the shaft. 2 in.- 7 (ksi) 12 Y (rad) 0.0006 0.0048
Fill Out this transaction Table showing all transaction anyalsis on the table. Transaction Dec 2 - A. Sayeed withdrew $2 000 from the business for personal use. Dec 4 - Purchased parts for repairing...
Your client is an individual who is the sole shareholder of a private corporation that is not a CCPC. The client expects the corporation's income and expenses for the coming year to be as follows:...
Using the SEC 10-K report for Vertex pharmaceuticals please respond to the following: What is the name of the auditor? Are they one of the "Big Four"? conduct a search to see who the "Big Four" audit...

A curve C in three dimensions is given parametrically by (x(t), y(t), z(t)), where t is a

Question:

XXoy- Yo = xo Yo z - Zo zo

Step by Step Answer:

The direction ...View the full answer

Modern Engineering Mathematics

Students also viewed these Sciences questions