A frame tent has a square of side 2 m and two semicircular cross members, FBE and GBD, as shown in Figure 8.88.

(a) Show that the cross-section ABC has equation 2x² + z² = 2

(b) Show that the capacity of the tent is 8√2/3m³.

Figure 8.88

(c) Show that the surface area S m² of the tent is given by

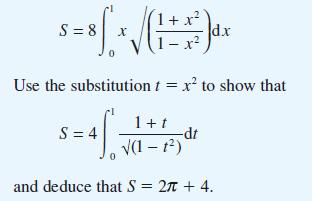
(d) Show that the length s* m of the arclength AB is given by

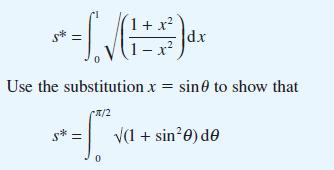
and evaluate (to 3dp) this integral using the trapezium rule.

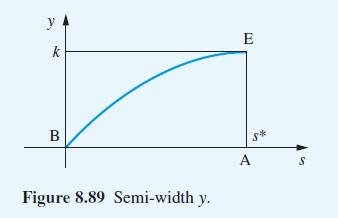
(e) We wish to compute the shape of one of the panels, BDE, of the tent. Show that the semiwidth y, at a distance s from B and illustrated in Figure 8.89, satisfies the differential equation

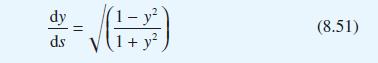
with y = 0 at s = 0.

(f) Show that the slope of the line OR is

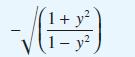
and explain why the construction described in (f) generates an approximate solution to the differential equation.
(g) Use the method to obtain a graphical solution to the differential equation. (Use A4 graph paper with a step size PP´ of 2 cm.)

(h) To use Euler’s method to compute the solution, it is easiest to rescale the independent variable s by setting s = s*t where 0 ≤ t ≤ 1. Show that the initialvalue problem becomes

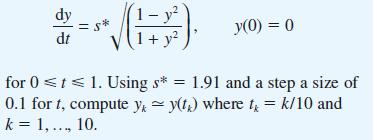
F G B D E [T]