(a) In Example 12.7 we saw that the periodic function

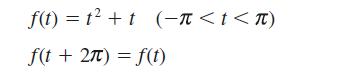
has a Fourier series expansion

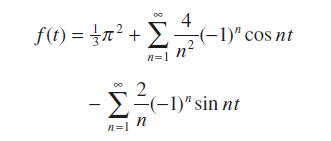
Differentiate this series term by term, and explain why it is not a Fourier expansion of the periodic function

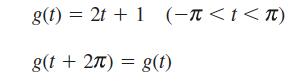
(b) Use the results of (a) to obtain the Fourier series expansion of g(t) and confirm your solution by direct evaluation of the coefficients using Euler’s formulae.

Data from Example 12.7

Suppose that g(t) and h(t) are periodic functions of period 2 and are defined within the
period –π

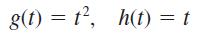
Determine the Fourier series expansions of both g(t) and h(t) and use the linearity property to confirm the expansion obtained for the periodic function f(t) defined within the period

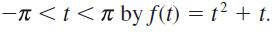
f(t)=t + t (- < t