Consider the integral where n is an integer. Using the trigonometric identity 1 + tan 2 x
Question:
Consider the integral
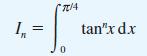
where n is an integer. Using the trigonometric identity 1 + tan2x = sec2x, show that
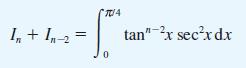
and hence obtain the recurrence relation
Use this to find
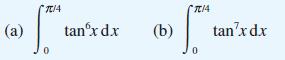
(Recurrence relations of this type are often called reduction formulae, since they provide a systematic way of reducing the value of the parameter n so that a difficult integral may be reduced to an easier one.)
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
a b Now So In 1In1 4 4 tan ...View the full answer
Answered By
Simon kingori
I am a tier-one market researcher and content developer who has been in this field for the last six years. I’ve run the freelancing gamut; from market research, data mining and SEO/SMM to copywriting, Content Development, you name it, I’ve done it. I’m extremely motivated, organized and disciplined – you have to be to work from home. My experience in Freelancing is invaluable- but what makes me a cut above the rest is my passion to deliver quality results to all my clients- it’s important to note, I've never had a dissatisfied client. Backed by a Masters degree in Computer Science from MOI university, I have the required skill set and burning passion and desire to deliver the best results for my clients. This is the reason why I am a cut above the rest. Having taken a Bsc. in computer science and statistics, I deal with all round fields in the IT category. It is a field i enjoy working in as it is dynamic and new things present themselves every day for research and exploration.
1+ Reviews
10+ Question Solved
Related Book For 
Question Posted:
