Using Laplace transform methods, solve for t ≥ 0 the following differential equations, subject to the specified initial conditions.

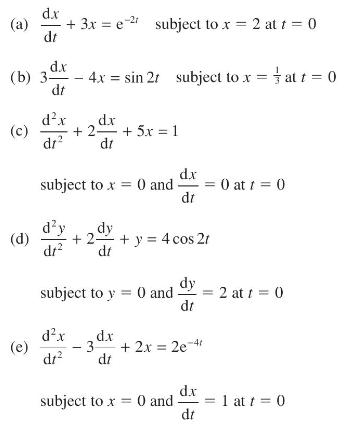
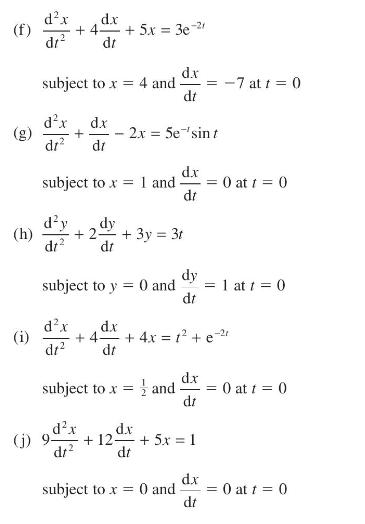
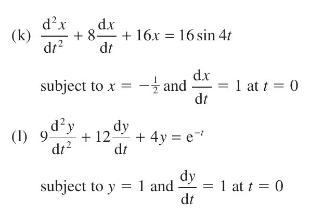
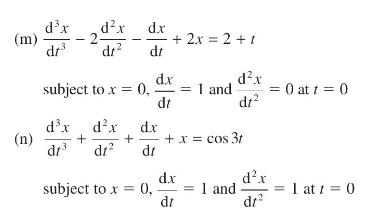
(a) (c) d.x + 3x = e2 subject to x = 2 at t = 0 dt (b) 3- d.x (e) dt dx dr - 4x = sin 2r subject to x = at t = 0 +2^^+5r=1 2dx dr subject to x = 0 and (d) +2 - + y = 4 cos 21 dy dt dx dr subject to y = 0 and dx - 3- dt d.x dr subject to x = 0 and dy dt + 2x = 2e-4t d.x dt 0 at t = 0 2 at 1 = 0 1 at t = 0