(a) Divide the integers up into four equivalence classes, Show that {e, a, b, c} form a group (left(mathrm{Z}_{4} ight)), under addition modulo 4 by

(a) Divide the integers up into four equivalence classes,

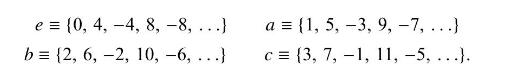
Show that {e, a, b, c} form a group \(\left(\mathrm{Z}_{4}\right)\), under addition modulo 4 by constructing the multiplication table. Hint: Recall that in addition modulo \(N\) two integers are added normally and then an integer multiple of \(N\) is added or subtracted to bring the result into the range \(-N\) to \(+N\). For example, \(3+2 \bmod 4=1\).

(b) Show that the matrices

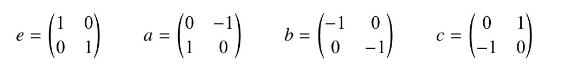
are a representation of \(Z_{4}\) under matrix multiplication.

(c) Define a homomorphism between \(\mathrm{Z}_{4}\) and the cyclic group \(\mathrm{C}_{4}\) of rotation operations in a plane {e, a, b, c\}, with \(e \equiv\) rotate by an integer multiple of \(2 \pi, a \equiv\) rotate counterclockwise by \(\frac{\pi}{2}, b \equiv\) rotate counterclockwise by \(\pi\), and \(c \equiv\) rotate counterclockwise by \(\frac{3 \pi}{2}\), by showing that \(\mathrm{Z}_{4}\) and \(\mathrm{C}_{4}\) have equivalent multiplication tables.

(d) Elements of \(Z_{N}\) may be represented by \(z_{i}=\exp (2 \pi i n / N)\) with \(n=0,1, \ldots, N-1\). Construct this representation for \(\mathrm{Z}_{4}\) and show that it has the same multiplication table as that obtained above for \(\mathrm{Z}_{4}\) and \(\mathrm{C}_{4} .

e = {0, 4, 4, 8, -8, ...) b= {2, 6, -2, 10, -6, ...) a = {1, 5, -3, 9, -7, ...) c = {3, 7, 1, 11, -5, ...).