For coordinates (left(x^{1}, x^{2} ight)) and metric (g=operatorname{diag}left(g_{11}, g_{22} ight)), the Gaussian curvature is For a sphere

For coordinates \(\left(x^{1}, x^{2}\right)\) and metric \(g=\operatorname{diag}\left(g_{11}, g_{22}\right)\), the Gaussian curvature is

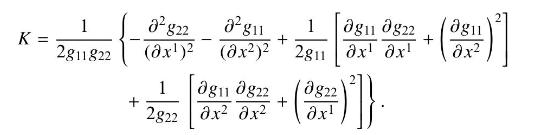
For a sphere with coordinates defined in the following figure,

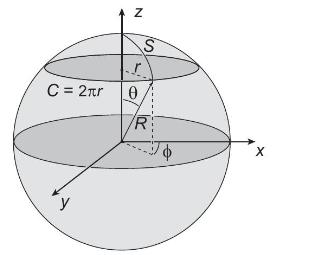
show that a Gaussian curvature \(K=R^{-2}\) is obtained using spherical coordinates \(\left(x^{1}, x^{2}\right)=(S, \phi)\) or cylindrical coordinates \(\left(x^{1}, x^{2}\right)=(r, \phi) .

Transcribed Image Text:

1 ag22 ag11 1 ag11 g22 agn K + 2811822 (x1) (x)2 1 811 822 2811 x x ax + ag22 + + 2822 x2 x2