Question: Show that for a continuous parameter (theta) the set of matrices forms a one-parameter abelian Lie group under matrix multiplication, and that if the matrices

Show that for a continuous parameter $\theta$ the set of matrices

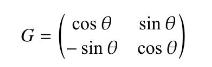
cos e G = sin 0 sin 0 cos 0)

forms a one-parameter abelian Lie group under matrix multiplication, and that if the matrices $G$ operate on a 2D cartesian space $\left(x_{1}, x_{2}\right)$ they leave $x_{1}^{2}+x_{2}^{2}$ invariant.

cos e G = sin 0 sin 0 cos 0)

Step by Step Solution

★★★★★

3.53 Rating (146 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The produc... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Physics Questions!

FIN 332 Integrative Case Study You have been asked to evaluate proposal to expand one of X Co's existing plants and make recommendations. X Co. produces batteries and sells them by the case. Proposal...

Portray in words what transforms you would have to make to your execution to some degree (a) to accomplish this and remark on the benefits and detriments of this thought.You are approached to compose...

Q1. You have identified a market opportunity for home media players that would cater for older members of the population. Many older people have difficulty in understanding the operating principles...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

For monotone functions f, f0: P Q between posets (P, vP ) and (Q, vQ), let f v f(i) Prove that the binary relation v is a partial order. [3 marks] (ii) For monotone functions between posets p : P 0...

Suppose that R(A, B, C) is a relational schema with functional dependencies F = {A, B C, C B}. (i) Is this schema in 3NF? Explain. [2 marks] (ii) Is this schema in BCNF? Explain. [2 marks] (b)...

lup ] (d) Show how a generating (or "mother") wavelet (x) can spawn a family of "daughter" wavelets jk(x) by simple shifting and scaling operations, and explain the advantages of representing...

year 2020 are as followS. CULLUMBER INC. BALANCE SHEETS Dec. 31, 2020 Jan. 1, 2020 Inc./Dec. Assets Cash $46,260 $14,260 $32,000 Inc. Accounts receivable 94,980 90,720 4,260 Inc. Equipment 42,980...

Explain why you might expect the MSE to be smaller in Question 2 than in Question 1.

Think back through Sofia path towards a more diversified portfolio what did it teach you about the portfolio management and responsibility I eating?

First, filter out all batters with fewer than 100 at bats. Next, standardize all the numerical variables using z-scores.

As the director of the multistate tax planning department of a consulting firm, you are developing a brochure to highlight the services it can provide. Part of the brochure is a list of five or so...

Castle Corporation conducts business in States 1, 2, and 3. Castle's $630,000 taxable income consists of $555,000 apportionable income and $75,000 allocable income generated from transactions...

Complete the following chart by indicating whether each item is true or false. Explain your answers by referencing the overlap of rules appearing in Federal and most state income tax laws. True or...

Consider the following Income statement for the Heir Jordan Corporation: HEIR JORDAN CORPORATION Income Statement $42,000 32,800 Sales Costs Taxable income Taxes (24%) $ 9,200 2,208 Net Income $...

Finish the Budget spreadsheet DO NOT CHANGE ANY FORMULAS! Change LastName . # in cell a 1 to your last name and dot number I have entered the appropriate taxes and other deductions for a single...

ConocoPhillips Spin-off of Phillips 66 - Need help with Q4 & 5.