The real numbers form a group under the binary operation of arithmetic addition. Show that for real numbers \(v\) the matrices

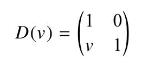
form a 2D representation of this additive group of real numbers. Show that transformation by this matrix corresponds to the Galilean transformations of classical physics, \(x^{\prime}=x+v t\) and \(t^{\prime}=t\), relating time and coordinate \((t, x)\) for one observer to time and coordinate \(\left(t^{\prime}, x^{\prime}\right)\) for an observer with relative velocity \(v\) along the \(x\)-axis.

D(v) = = (9)