Using the commutators for \(J_{i}\) and \(K_{i}\) given in Problem 3.8 , argue that the \(\mathrm{SO}(4)\) Lie algebra is semisimple, but not simple. Argue that \(\mathrm{SO}(4)\) can be written as a direct product of two simple groups, which can be analyzed independently.

Data from Problem  3.8

Show that for a four-dimensional cartesian space \((x, y, z, t)\) the operators

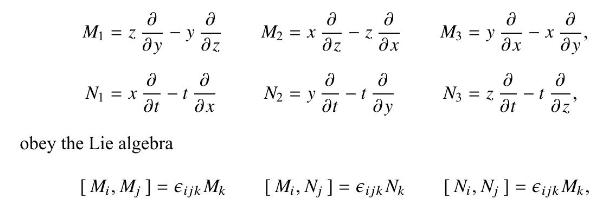
which is the algebra associated with the group \(\mathrm{SO}(4)\). Show that this \(\mathrm{SO}(4)\) is locally isomorphic to \(\mathrm{SU}(2) \times \mathrm{SU}(2)\) by showing that the new operator set,

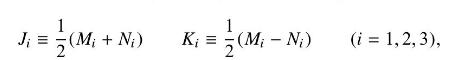
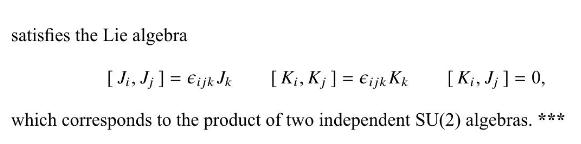
M = z a a a y M = x - M3 = y x z z a N = y - 1 a - N3 = 2 - - t N = X a - - obey the Lie algebra [Mi, M;] Eijk Mk [Mi, Nj] = ijk Nk [Ni, Nj] = Eijk Mk,