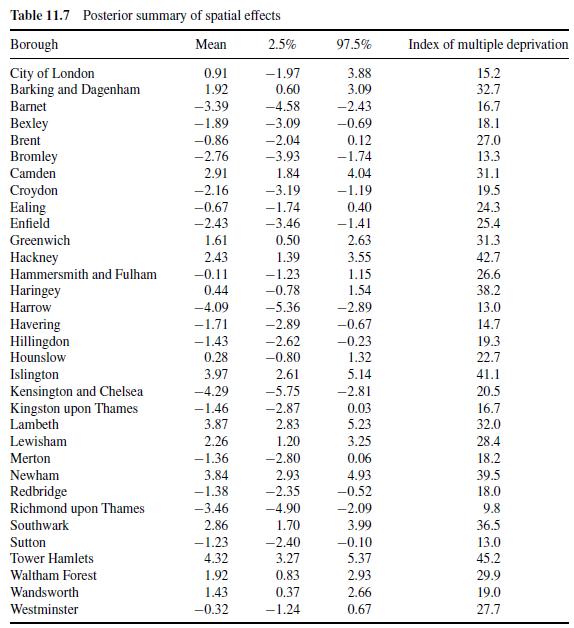
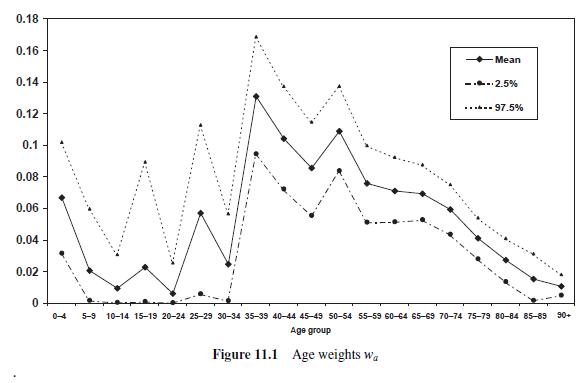
Question: 1. For the data in Example 11.1 consider a heteroscedastic model for the level 1 random effects (the overdispersion error ei j ) involving the
1. For the data in Example 11.1 consider a heteroscedastic model for the level 1 random effects (the overdispersion error ei j ) involving the binary borough group indicator wj
(wj = 1 for inner boroughs). Thus
![log(ij)=b+b;2(xij - x) + eij, (b1, b2) ~ N2([mj1, mj2], b), mj1](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1730/9/7/4/680672c93d8b236c1730974471548.jpg)
For example a possible code using a stacked data arrangement with borough indicators Gi could be

Informative priors on θ j (e.g. θ j ∼ N(0, 1)) are suggested, and initial values compatible with a positive variance (and precision).
log(ij)=b+b;2(xij - x) + eij, (b1, b2) ~ N2([mj1, mj2], b), mj1 = 811 +812wj, mj2 = 821 +822Wj, eij~ N(0, Vij), Vij = 0+02wj.
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


