10.2. (Sec. 10.2)

(a) Let y(g), g = 1, ... , q, be a set of random vectors each with p components.

Suppose

Let C be an orthogonal matrix of order q such that each element of the last row is

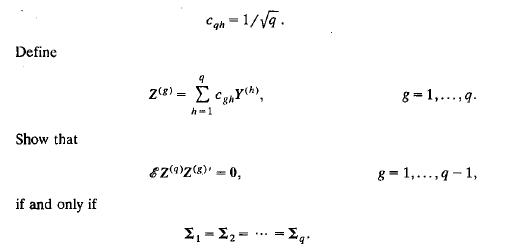
(b) Let x~g), a = 1, ... , N, be a random sample from N(IL(g), :Ig), g = 1, ... , q.
Use the result from

(a) to construct a test of the hypothesis

based on a test of independence of Z(q) and the set Z(l), •.• , Z(q-I). Find the exact distribution of the criterion for the case p = 2.

Y(8)=0, Y(8)(h)=8gg -