3.11. (Sec. 3.2) Estimation of parameters of a complex normal distribution. Let ZI"'" ZN be N obseIVations from the complex normal distributions with mean 6 and covariance matrix P. (See Problem 2.64.)

(a) Show that the maximum likelihood estimators of 0 and Pare

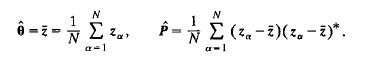
(b) Show that Z has the complex normal distribution with mean 6 and covariance matrix (l/N)P.

(c) Show that z and P are independently distributed and that NP has the distribution of r.:_ 1 Wa Wa*' where WI"'" w" are independently distributed, each according to the complex normal distribution with mean 0 and covariance matrix P, and n = N - 1.

-- N N (za-)(za-)*.