4. Consider the normal linear non-differential measurement error model for i = 1, . . . , n xi N(Xi , 1/), yi

4. Consider the normal linear non-differential measurement error model for i = 1, . . . , n xi ∼ N(Xi , 1/τδ), yi ∼ N(β0 + β1Xi + β2Zi , 1/τε), Xi ∼ N(α0 + α1Zi , 1/τη).

Assume flat priors for {α0, α1, β0, β1, β2}, namely P(α0) ∝ 1, etc. Also assume Ga(1, 1)

priors on τδ, τε and τη. The posterior density of these parameters and the unknown X are proportional to

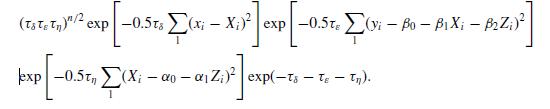
Obtain the full conditional densities for the regression and precision parameters and the true X values. Also derive these densities for informative priors on {α0, α1, β0, β1, β2}, e.g. normal priors α0 ∼ N(A0, Va0), and general gamma priors on the precisions, e.g. τδ ∼
Ga(0.5νδ, 0.5Sδ ).

(tste tn)" exp-0.5ts (x;-X;) exp | -0.5te (yi - Bo - BX; BZ;) | exp -0.5t (X-ao-a1Zi) exp(-ts-T - Tn).