4. Generate 100 points from the mixture f (x) = (x|0.15, 0.05)/4 + (x|0.6, 0.2)/4, where (x|,) is the normal density with mean and

4. Generate 100 points from the mixture f (x) = φ(x|0.15, 0.05)/4 + φ(x|0.6, 0.2)/4, where φ(x|μ,κ) is the normal density with mean μ and standard deviation κ and add a normal random error with mean 0 and variance 1 to give a noisy version yi = f (xi ) + εi of the true function f (x). The true curve peaks at f (0.175) ∼=

2, and tails off rapidly being flat at f (x) ∼=

0.3 after x = 0.25.

Select K = 19 knots placed at the 5th, 10th, . . . , 95th percentiles of the observed (i.e.

sampled) x. With a cubic spline model, first apply a regression selection to the coefficients at each knot, with

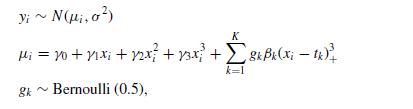
where βk as fixed effects. Second, apply the penalised random effects method for βk(Section 10.5.1) without coefficient selection. Which method better reproduces the underlying true series f (x) and which is more complex?

yi~ N(i, ) K M = 20 + 1 x + 12x + 13x+8kBx(x; - 1k) k=1 gk 8k ~ Bernoulli (0.5),