5.7. Let {Xn,t,An,t} be a martingale difference sequence. Suppose the Lindeberg condition: Xn t=1 E{X2 n,t(|Xn,t| > )} 0, (n ), for every

5.7. Let {Xn,t,An,t} be a martingale difference sequence. Suppose the Lindeberg condition:

Xn t=1 E{X2 n,tχ(|Xn,t| > ε)} → 0, (n → ∞), for every ε > 0.

Then, show the following (i) and (ii):

(i) max 1≤t≤n

|Xn,t| p→

0,

(ii) there exists M > 0 satisfying

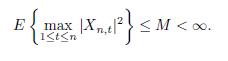
Xnt M. E max Xntl 1