The centered finite difference formulas can be written in the form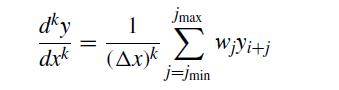

where k is the order of the derivative and the values of j denote locations relative to node i. For this problem, we will consider the lowest-order form for the fourth derivative using the Taylor series approach.

(a) Write out the Taylor series expansion for an arbitrary number of nodes j away from node i.

(b) What is the smallest range j ∈ [j_min, j_max] that can be used to compute the centered fourth derivative?

(c) How many equations are required to determine the weights w_j?

(d) Using the results from parts (a)–(c), develop a system of algebraic equations that would allow you to solve for the weights w_j.

dky dxk 1 (.x) jmax wiviti j=jmin