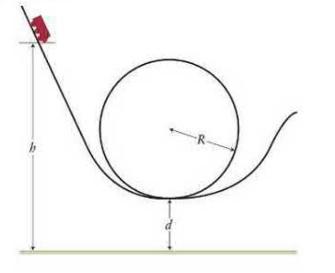
A roller-coaster car initially at a position on the track a height \(h\) above the ground begins a downward run on a long, steeply sloping track and then goes into a circular loop-the-loop of radius \(R\) whose bottom is a distance \(d\) above the ground (Figure P11.37). Ignore friction.

(a) What is the car's speed when it reaches the bottom of the loop?

(b) What is the magnitude of the normal force exerted on the car at that instant?

(c) What is its speed when its position is one-quarter of the way around the loop?

(d) What is the magnitude of the normal force exerted on it at the one-quarter position?

(e) What is the car's acceleration at the one-quarter position?

Data from Figure P11.37