A spring \((k=3800 \mathrm{~N} / \mathrm{m})\) is compressed between two blocks: block 1 of inertia \(1.40 \mathrm{~kg}\) and block 2 of inertia \(2.00 \mathrm{~kg}\). The combination is held together by a string (not shown in Figure P10.63). The combination slides without spinning across low-friction ice at \(2.90 \mathrm{~m} / \mathrm{s}\) when suddenly the string breaks, allowing the spring to expand and the blocks to separate. Afterward, the 2. 00\(\mathrm{kg}\) block is observed to move at a \(34.0^{\circ}\) angle to its initial line of motion at a speed of \(3.50 \mathrm{~m} / \mathrm{s}\), while the smaller block moves off at an unknown speed and angle. Neither block is rotating after the separation, and you can ignore the inertias of the spring and the string relative to those of the blocks.

(a) Determine the velocity of block 1 after the separation.

(b) Determine the original compression of the spring, \(y-y_{0}\), from its relaxed length \(y\).

Data from Figure P10.63

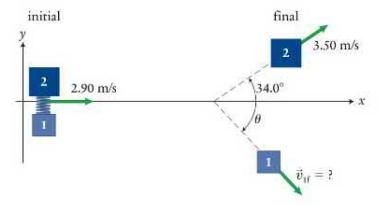
initial final 2 3.50 m/s 2.90 m/s 34.0 +x