The angular frequency \(\omega\) of a simple pendulum can be calculated by treating the pendulum as a one-dimensional oscillator. In Section 15.4, we used this approach to analyze the restoring force exerted on a pendulum, considering the effect of the force of gravity on the horizontal displacement of the bob and ignoring the slight difference between the horizontal displacement \(x\) and the are length \(s\) along which the bob swings. Show that this treatment yields for \(\omega\) the same expression I obtained in Example 15.6, \(\omega=\sqrt{g / \ell}\).

Data from Section 15.4

..............

Data from Example 15.6

Suppose a simple pendulum consisting of a bob of mass \(m\) suspended from a string of length \(\ell\) is pulled back and released. What is the period of oscillation of the bob?

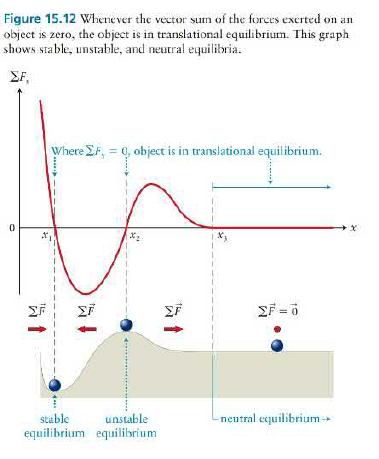
Periodic motion takes place about a position of trans- lational or rotational equilibrium (see Section 12.5) and requires a restoring force that tends to return the object to the equilibrium position. Consider, for exam- ple, an object moving along an x axis and subject to the vector sum of forces whose x component is shown graphically in Figure 15.12. The object is in transla- tional equilibrium at each position where the vector sum is zero: at x1, x2, and all values of x > x3. Can the object oscillate about any of these positions? From the graph we see that F, is positive to the left of x, and so the vector sum F points toward x1. To the right of x1, F is negative, and so the vector sum of forces