Assume a joint distribution px, y of two random vectors x 2 Rn and y 2 Rn is a linear Gaussian model defined as follows:

Assume a joint distribution p¹x, yº of two random vectors x 2 Rn and y 2 Rn is a linear Gaussian model defined as follows:

p¹xº = N

????

x

, ????1

, where 2 Rn is the mean vector; 2 Rnn is the precision matrix; and p¹y j xº = N

????

y Ax +

b, L????1

, where A 2 Rnn, b 2 Rn, and L 2 Rnn is the precision matrix. Derive the mean vector and covariance matrix of the marginal distribution p¹yº in which the variable x has been integrated out.

Hints: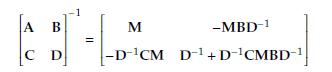 

with M = ????
A???? BD????1C ????1.

B M [A CD -MBD-1 -DCM D1 + D-CMBD-1