Consider an m-dimensional variable r, whose elements are nonnegative integers. Suppose its distribution is described by a mixture of multinomial distributions:

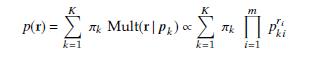
where the parameter pki denotes the probability of ith dimension in the kth component, subject to 0 pki 1 (8k, i) and Í
i pki = 1 (8k). Assume a set of training samples is given as
r¹nº
n = 1, , N
.
Derive the E-step and M-step of the EM algorithm to optimize the mixing weights fk g (
Í
k k = 1) and all component parameters fpki g based on the MLE.

P(r) = K k Mult(r|Pk) o k=1 m ck k=1 i=1