Given a set of training samples DN =

x1, x2, , xN

, the so-called empirical distribution corresponding to DN is defined as follows:

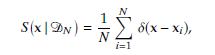
where ¹º denotes Dirac’s delta function. Show that the MLE is equivalent to minimizing the Kullback–
Leibler (KL) divergence between the empirical distribution and the data distribution described by a generative model pˆ¹xº:

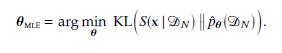
S(x DN) 8(x-x1), N i=1